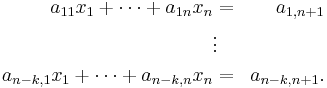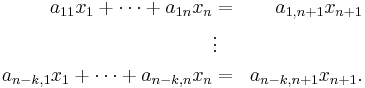Affine Grassmannian (manifold)
In mathematics, there are two distinct meanings of the term affine Grassmannian. In one it is the manifold of all k-dimensional affine subspaces of Rn (described on this page), while in the other the affine Grassmannian is a quotient of a group-ring based on formal Laurent series.
Formal definition
Given a finite-dimensional vector space V and a non-negative integer k, then Graffk(V) is the topological space of all affine k-dimensional subspaces of V.
It has a natural projection p:Graffk(V) → Grk(V), the Grassmannian of all linear k-dimensional subspaces of V by defining p(U) to be the translation of U to a subspace through the origin. This projection is a fibration, and if V is given an inner product, the fibre containing U can be identified with 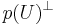 , the orthogonal complement to p(U). The fibres are therefore vector spaces, and the projection p is a vector bundle over the Grassmannian, which defines the manifold structure on Graffk(V).
, the orthogonal complement to p(U). The fibres are therefore vector spaces, and the projection p is a vector bundle over the Grassmannian, which defines the manifold structure on Graffk(V).
As a homogeneous space, the affine Grassmannian of an n-dimensional vector space V can be identified with
where E(n) is the Euclidean group of Rn and O(m) is the orthogonal group on Rm. It follows that the dimension is given by
Relationship with ordinary Grassmannian
Let (x1,…,xn) be the usual linear coordinates on Rn. Then Rn is embedded into Rn+1 as the affine hyperplane xn+1 = 1. The k-dimensional affine subspaces of Rn are in one-to-one correspondence with the linear subspaces of Rn+1 that are in general position with respect to the plane xn+1 = 1. Indeed, a k-dimensional affine subspace of Rn is the locus of solutions of a rank n k system of affine equations
These determine a rank n−k system of linear equations on Rn+1
whose solution is a (k+1)-plane that, when intersected with xn+1 = 1, is the original k-plane.
Because of this identification, Graff(k,n) is a Zariski open set in Gr(k+1,n+1).
References
- Klain, Daniel A.; Rota, Gian-Carlo (1997), Introduction to Geometric Probability, Cambridge: Cambridge University Press
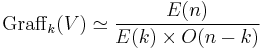
![\dim\left[ \mathrm{Graff}_k(V) \right] = (n-k)(k-1) \, .](/2012-wikipedia_en_all_nopic_01_2012/I/409af1f323bf0c34e757e16485f54364.png)